Markov Decision Process
(2025-11-14T16:27.289Z)
Perplexity Query
(2025-11-14T16:27
.289Z)
Question:
Write a comprehensive one-page article about "Markov Decision Process".
Model: sonar-pro
A Markov Decision Process (MDP) is a mathematical framework used for modeling decision-making situations where outcomes are partly random and partly within the control of a decision-maker[1][2]. MDPs are crucial in many fields, including artificial intelligence (AI), operations research, and economics, because they enable systematic analysis of sequential decisions under uncertainty—a fundamental challenge in developing autonomous systems, optimizing operations, and strategic planning[4][7].
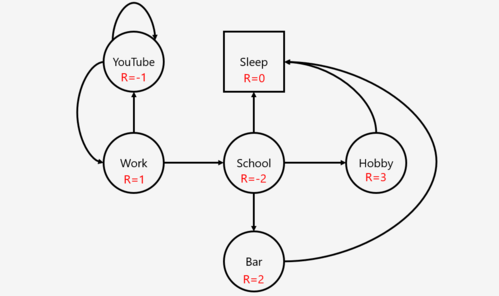
Main Content
At its core, an MDP models a system by defining a set of states, a set of actions available to the decision-maker, transition probabilities that describe the likelihood of moving between states given a chosen action, and a reward function that assigns immediate value or cost to each action in each state[5][6]. The “Markov property” means the next state depends only on the current state and action—not on the sequence of events that preceded it[2][4]. This simplification allows for powerful mathematical techniques and efficient computation of optimal policies, where a policy is a strategy for choosing actions based on the current state[1].
Practical Examples and Use CasesMDPs are foundational to reinforcement learning, an area of machine learning where agents learn to make decisions through trial and error, receiving feedback in the form of rewards[4].
- In robotics, an MDP might guide a robot to navigate unfamiliar environments while avoiding obstacles and reaching specific goals[4].
- Autonomous vehicles use MDPs to make real-time driving decisions, such as when to accelerate, brake, or change lanes, by evaluating possible future traffic scenarios[4][5].
- In healthcare, doctors can use MDPs to sequence treatments for chronic illnesses, choosing actions that maximize the patient’s expected health outcome in the face of uncertain responses[3][5].
- Operations management and finance commonly use MDPs for tasks like inventory control, where the system helps decide when to reorder stock considering fluctuating demand and supply uncertainties[3][5].
The benefits of MDPs include their versatility, ability to structure complex sequential decision problems, and suitability for real-time, automated decision-making in environments that change unpredictably[1][4]. However, challenges remain: real-world problems often have enormous or continuous state spaces, making computation of optimal policies computationally demanding (the “curse of dimensionality”). Additionally, estimating transition probabilities and rewards accurately from real data can be a complex task, especially in dynamic or poorly understood environments[4].
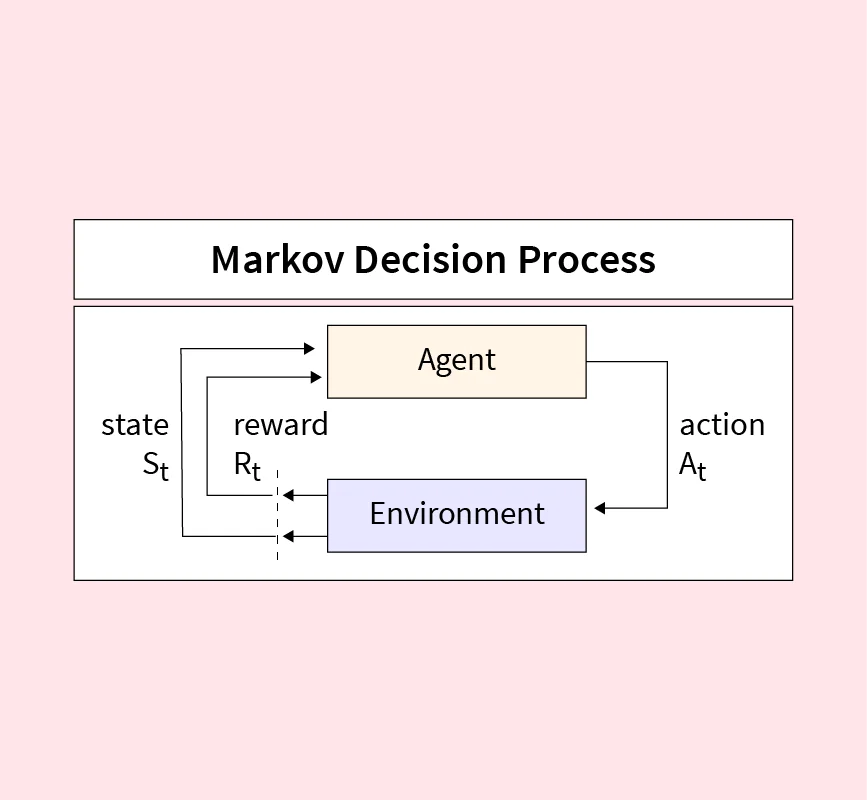
Current State and Trends
MDPs are widely adopted in academia and industry, underpinning the success of many cutting-edge technologies in AI, robotics, automated trading, logistics, and intelligent planning[4]. They serve as the mathematical backbone for reinforcement learning algorithms powering famous achievement like AlphaGo’s victory in the board game Go, and real-world implementations in self-driving cars and smart resource allocation in data centers[4][5][7]. Key players in the market include technology giants such as Google, Amazon, and Tesla, who apply MDP frameworks extensively in AI research and applications.
Recent trends focus on improving scalability, such as through approximate dynamic programming, deep reinforcement learning (which combines neural networks and MDPs), and using MDP variants suited for large or continuous state spaces (like partially observable MDPs, or POMDPs)[4][8]. Research communities are actively exploring how to interpret, explain, and make these decision-making systems more transparent, especially for applications in healthcare, autonomous vehicles, and other high-stakes domains[3].
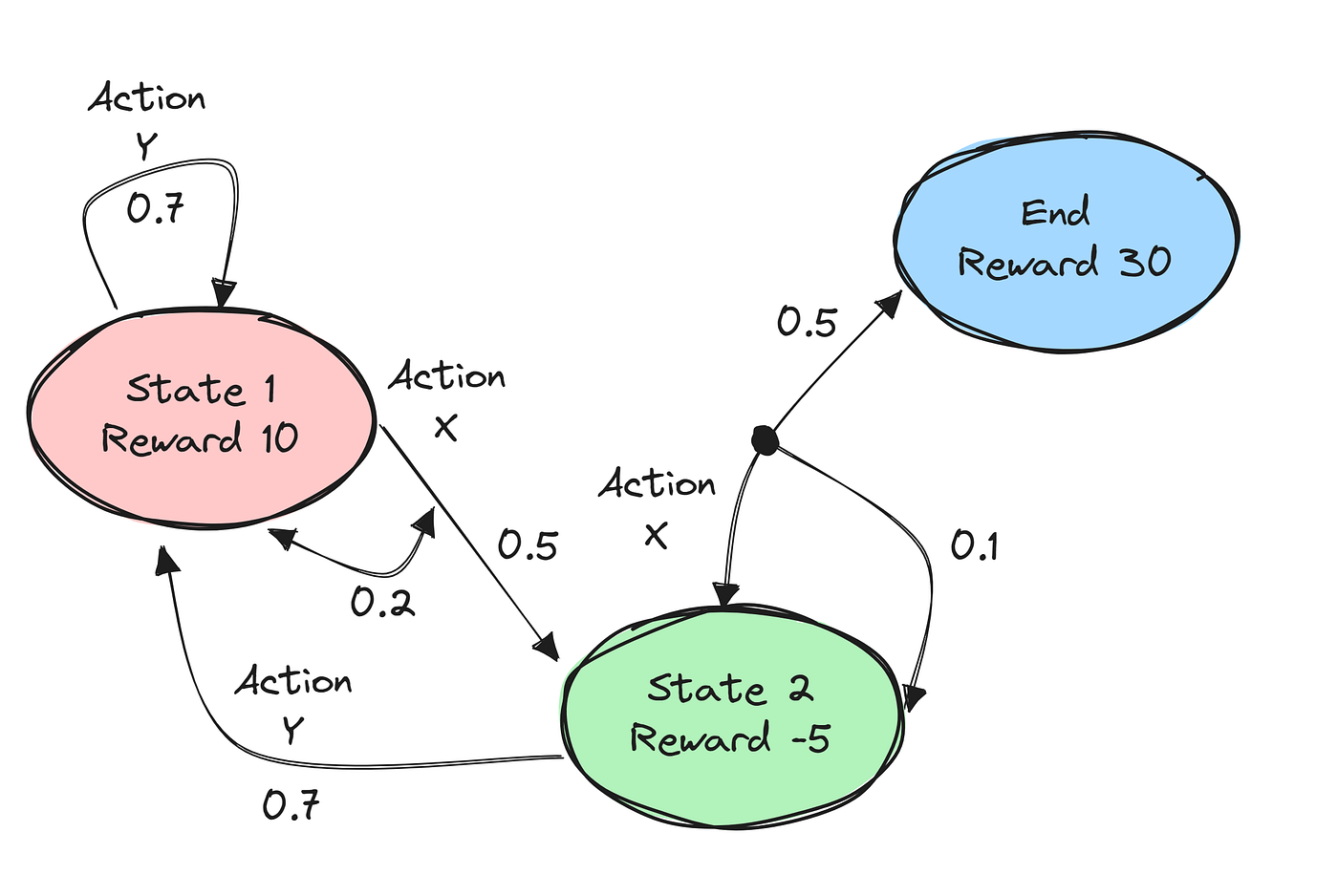
Future Outlook
Looking ahead, Markov Decision Processes are expected to become even more integral as AI systems are deployed in complex, real-world settings—from personalized medicine to fully autonomous transportation and beyond. Advances in computational power, efficient algorithms, and integration with big data will allow MDPs to solve increasingly sophisticated problems, while new research will address interpretability and ethical decision-making[8]. This intersection of mathematical rigor and real-time learning promises to reshape how organizations and intelligent machines plan, adapt, and thrive in dynamic environments.
Conclusion
Markov Decision Processes provide a powerful, flexible approach for modeling and optimizing sequential decisions under uncertainty. As technology and data continue to advance, MDPs will remain central to the development of smarter, more adaptive systems capable of tackling complex real-world challenges.
Citations
[2]: 2025, Nov 14. Understanding the Markov Decision Process (MDP) - Built In. Published: 2024-08-13 | Updated: 2025-11-14
[3]: 2025, Nov 13. Markov Decision Processes: A Tool for Sequential Decision Making .... Published: 2009-12-31 | Updated: 2025-11-13
[4]: 2025, Nov 14. Exploring Markov Decision Processes: A Comprehensive Survey of .... Published: 2024-07-04 | Updated: 2025-11-14
[5]: 2025, Nov 14. Markov Decision Process - GeeksforGeeks. Published: 2025-10-09 | Updated: 2025-11-14
[8]: 2025, Nov 14. 11 Markov Decision Processes – 6.390 - Intro to Machine Learning. Published: 2021-01-01 | Updated: 2025-11-14